6用于中长期天气预报的二元二次曲线图
二元二次回归模型的数学表达式可写成:
Y =A0 + A1•X1 + A2•X2 + A12•X1•X2 + A11•X12 + A22•X22 ……(3)
(3)式中,X1、X2为自变量,Y为因变量, A0、A1、A2、A12、A11、A22为参数(即回归系数),参数可通过回归分析求出。
在“农业气象信息及天气预报工具平台”中大部分模型图都是彩色的,在本文中都将彩色改成了黑白色。对于图17、18、19、20,由于黑白图中等直线(曲线或直线)的数值标注可能看不太清楚,现特作如下说明:
图17、18都是用二元二次回归方法制作天气预报的模型图。其中,图17是黑龙江垦区某地用大前年7月降水量(X1)和大前年12月降水量(X2)预报当年8月降水量的二元二次回归预报图,纵坐标为X1,横坐标为X2。图中的曲线为当年8月降水量预报等值线(其中,最内圈等值线的值为76.1MM,次圈为135.6MM,最外圈为611.7MM,共10圈,详见图中标注)。图中,最内圈中是预报当年8月降水最少(少于76.1MM)的区域。统计数据表明,这个预报方法,回归标准误差为44.6MM。
图18是黑龙江垦区某地用去年12月降水量(X1)和去年11月降水量(X2)预报当年7月降水量的二元二次回归预报图,纵坐标为X1,横坐标为X2。图中的曲线为当年7月降水量预报等值线(其中,最内圈等值线的值为213.1MM,次圈为190.7MM,最外圈为11.2MM,共10圈,详见图中标注)。从图中可以看出,当去年12月降水量X1少(比如,少于5MM),且去年11月降水量X2多时(比如,大于62MM),可预报当年7月降水量为多(213MM以上)。统计数据表明,这个预报方法,回归标准误差为30.2MM。
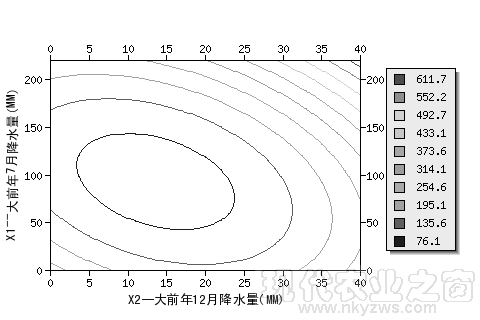
图17:黑龙江垦区某地8月降水量二元二次回归预报图
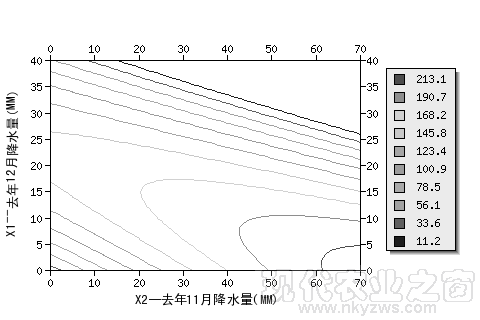
图18:黑龙江垦区某地7二元二次回归预报图月降水量
7 用于中长期天气预报的二元线性回归预报图
二元线性回归模型的数学表达式可写成:
Y =A0 + A1•X1 + A2•X2 ……(4)
(4)式中,X1、X2为自变量,Y为因变量, A0、A1、A2为参数(即回归系数),参数可通过回归分析求出。
图19、20都是用二元线性回归方法制作天气预报的模型图。其中,图19是黑龙江垦区某地用大前年5月降水量(X1)和大前年11月降水量(X2)预报当年6月降水量的二元线性回归预报图,纵坐标为X1,横坐标为X2。图中的10条直线为当年6月降水量预报等值线(其中,右下角一条直线的值为10.6MM,向上紧挨着的一条直线为23.3MM,最左上角的一条直线为124.6MM,详见图中标注)。统计数据表明,这个预报方法,回归标准误差为22.4MM。
图20是黑龙江垦区某地用去年9月降水量(X1)和去年11月降水量(X2)预报当年7月降水量的二元线性回归预报图,纵坐标为X1,横坐标为X2。图中10条直线为当年7月降水量等值线(其中,左下角的直线的值为92.2MM,挨着它的一条直线为108.1MM,右上角的一条直线为235.3MM,详见图中标注)。统计数据表明,这个预报方法,回归标准误差为37.5MM。
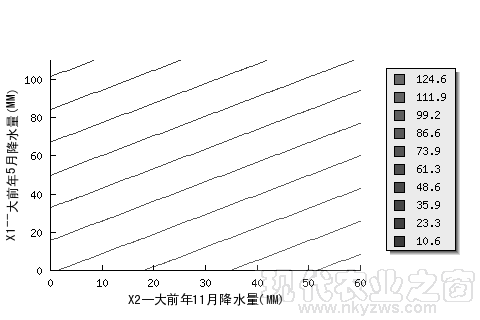
图19:黑龙江垦区某地6月降水量二元线性回归预报图
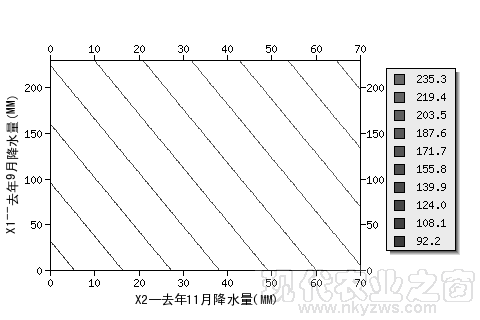
图20:黑龙江垦区某地7月降水量二元线性回归预报图
8 结束语
“农业气象信息及预报工具平台”就其内容尤如汪洋大海,本文虽然题目名字是《...理论和应用图全集》,但所介绍的也仅有20张经典图片,这些仍是沧海一粟,但愿对读者有些帮助!如果读者想得到更多的启发,请登录“现代农业之窗”网(http://www.nkyzws.com),在“生态气象”栏目,找到“农业气象信息及预报工具平台”,联系我们开通使用。
参考文献
[1]李宝华,李晓红,李德明. 降水对春小麦产量贡献率的研究,中国生态农业学报,第11卷第4期,161-162页,2003年10月.
[2]刘玉顺,李晓红,李德明. “农业气象信息及预报工具平台”理论和应用图集锦,现代化农业,2018年11期,2-4页,2018年11月.
致谢:此文在编写过程中,黑龙江垦区锦河、友谊、红色边疆、新华、宝山、赵光、格球山等农场气象站为我们提供了资料和分析数据,作者表示衷心感谢!
* 注:“农业气象信息及预报工具平台”原名“农业气象数据库信息服务系统”,由黑龙江省农垦科学院原生态气象室李德明主持,从1988年开始研制。1992年获黑龙江省农场总局科技进步二等奖,1993年获黑龙江省科技进步四等奖。2002年开发网络版,至今已是 “农业气象信息及预报工具平台2018版”。 30年来,许多基层气象台站都在使用。
“农业气象信息及预报工具平台”主持人:李德明,联系电话:15590919407;QQ:391039782 。
选看第(一、二、三、四、五)部分